Set Theory

Mathematics | Introduction of Set theory

A Set is an unordered collection of objects, known as elements or members of the set.
An element ‘a’ belong to a set A can be written as ‘a ∈ A’,  ‘a ∉ A’ denotes that a is not an element of the set A.

 Representation of a Set

A set can be represented by various methods. 3 common methods used for representing set:
1. Statement form.
2. Roaster form or tabular form method.
3. Set Builder method.

 Statement form

In this representation, the well-defined description of the elements of the set is given. Below are some examples of the same.
1. The set of all even number less than 10.
2. The set of the number less than 10 and more than 1.

 

Roster form
In this representation, elements are listed within the pair of brackets {} and are separated by commas. Below are two examples.
1. Let N is the set of natural numbers less than 5.
N = { 1 , 2 , 3, 4 }.

2. The set of all vowels in the English alphabet.
V = { a , e , i , o , u }.

 

Set builder form
In Set-builder set is described by a property that its member must satisfy.
1. {x : x is even number divisible by 6 and less than 100}.
2. {x : x is natural number less than 10}.

 

Equal sets
Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets. 

Subset

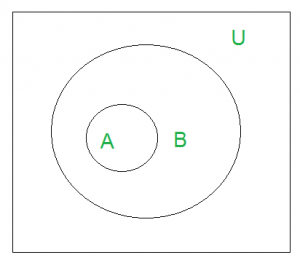
A set A is said to be subset of another set B if and only if every element of set A is also a part of other set B.
Denoted by ‘⊆‘.
‘A ⊆ B ‘ denotes A is a subset of B.

To prove A is the subset of B, we need to simply show that if x belongs to A then x also belongs to B.
To prove A is not a subset of B, we need to find out one element which is part of set A but not belong to set B.

asubsetB

‘U’ denotes the universal set.
Above Venn Diagram shows that A is a subset of B.

 Size of a Set

Size of a set can be finite or infinite.

For exampleSize of the set S is known as Cardinality number, denoted as |S|.

Example: Let A be a set of odd positive integers less than 10.
Solution : A = {1,3,5,7,9}, Cardinality of the set is 5, i.e.,|A| = 5.

Note: Cardinality of a null set is 0.

 

Power Sets
The power set is the set all possible subset of the set S. Denoted by P(S).
Example: What is the power set of {0,1,2}?
Solution: All possible subsets
{∅}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}.
Note: Empty set and set itself is also the member of this set of subsets.

 

Cardinality of power set is

2^n

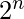
, where n is the number of elements in a set.

 Cartesian Products

Let A and B be two sets. Cartesian product of A and B is denoted by A × B, is the set of all ordered pairs (a,b), where a belong to A and b belong to B.

A × B = {(a, b) | a ∈ A ∧ b ∈ B}.

Example 1. What is Cartesian product of A = {1,2} and B = {p, q, r}.
Solution : A × B ={(1, p), (1, q), (1, r), (2, p), (2, q), (2, r) };


The cardinality of A × B  is N*M, where N is the Cardinality of A and M is the cardinality of B.

Note: A × B is not the same as B × A.

Cantor’s Development of Set Theory

In his development of set theory, Cantor identified a single fundamental principle, called the Comprehension Principle, under which one can form a set. Cantor’s principle states that, given any specific property \varphi(x) concerning a variable x, the collection \{x : \varphi(x)\} is a set, where \{x : \varphi(x)\} is the set of all objects x that satisfy the property \varphi(x). For example, let \psi(x) be the property that “x is an odd natural number.” The Comprehension Principle implies that

S = \{ x : \psi (x)\} = \{1,3,5,7,\ldots \} 

is a set. Employing the Comprehension Principle, one can form the intersection of two sets A and B using the property “x \in A and x \in B“; thus, the intersection of A and B is the set

A \cap B = \{x : x \in A and x \in B\}. 

One can also form the set

A \cup B = \{x : x \in A or x \in B\} 

which is called the union of A and B. Recall that one writes X \subseteq A to mean that X is a subset of A, that is, every element of X is also an element of A. Using the Comprehension Principle, one can form the power set of A, which is the set whose elements are all of the subsets of A, that is,

\wp(A) = \{ X : X \subseteq A\}. 

Thus, if A is a set and X \subseteq A, then X \in \wp(A). So, if A = \{1,2,3\} and B = \{3,4,5\}, then

A \cap B = \{3\},
A \cup B = \{1,2,3,4,5\}, and

\wp(A) = \{\varnothing,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\}, 

where \varnothing denotes the empty set, that is, the set that contains no elements. The Comprehension Principle was an essential tool that allowed Cantor to form many important sets. Cantor’s approach to set theory is often referred to as naïve set theory.

Cantor’s set theory soon became a very powerful tool in mathematics. In the early 1900s, the mathematicians Émile Borel, René-Loius Baire, and Henri Lebesgue used Cantor’s set theoretic concepts to develop modern measure theory and function theory (Kanamori 2012). This work clearly demonstrated the great mathematical utility of set theory